Системи бројева и услови

Три главна подручја разлике од наших бројева

Замислите колико би било лакше научити аритметику у првим годинама када би све што сте требали научити писати линију као што сам ја и троугао. То су у основи сви древни људи Месопотамије морали учинити, мада су их варирали ту и тамо, издужујући се, окрећући се итд.

Нису имали наше оловке и оловке или папир за ту ствар. Оно што су написали било је средство које ће се користити у скулптури, јер је подлога глина. Да ли је ово теже или лакше научити руковати него оловком је избацивање, али за сада су напред у одељењу за лакоћу, са само два основна симбола за научити.

Следећи корак је бацач кључа у одељење за једноставност. Користимо

У "Почаст Бабилонији" [Математички гласник, Вол. 76, бр. 475, „Употреба историје математике у настави математике“ (мар. 1992.), стр. 158-178], наставник писца Ницк Мацкиннон каже да користи вавилонску математику да подучава 13-годишњаке о основама које нису 10. Вавилонски систем користи базу-60, што значи да је уместо да буде децимална, сексуалан.

И бабилонски систем бројева и наш ослањају се на позицију да дају вредност. Два система то раде другачије, дијелом зато што њиховом систему недостаје нула. Учење бабилонског система лево-десно (високо до ниско) за први укус основне аритметике вероватно није више тешко него научити наш двосмерни, при чему морамо запамтити редослед децималних бројева - повећавајући се из децималног, оне, десетине, стотине, а затим навијају у другом смеру са друге стране, ни један ступац, само десетине, стотинке, хиљаде итд.

Прећи ћу на ставове вавилонског система на наредним страницама, али прво треба да се науче неке важне бројевне речи.

Говоримо о периодима година користећи децималне величине. Имамо деценију 10 година, век 100 година (10 деценија) или 10Кс10 = 10 година квадрат, и миленијум 1000 година (10 векова) или 10Кс100 = 10 година у кубама. Не знам никакав виши термин од тога, али то нису јединице које су користили Бабилонци. Ницк Мацкиннон се односи на таблет из Сенкареха (Ларса) од Сир Хенрија Ровлинсона (1810-1895) * за јединице које су користили Бабилонци и то не само за укључене године, већ и за подразумеване количине:

1. сосс
2. нерв
3. сар.

сосснерсосссарсосс

Још увијек нема прекидача за кравате: Није нужно лакше научити изведене изразе из квадратних и коцкастих година од латинског него што је то једносложни бабилонски језик који не укључује куцање, већ множење са 10.

Шта мислиш? Да ли би било теже научити основе броја као бабилонско школско дете или као савремени ученик у школи која говори енглески језик?

* Георге Равлинсон (1812-1902), Хенријев брат, показује поједностављену преписану таблицу квадрата у Седам великих монархија древног источног света. Чини се да је табела астрономска, заснована на категоријама вавилонских година.

Све фотографије потичу из ове скениране верзије издања Георгеа Ровлинсона из 19. века Седам великих монархија древног источног света.

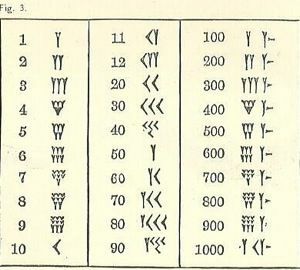
Пошто смо одрасли са другачијим системом, вавилонски бројеви су збуњујући.

Барем се бројеви крећу од висине са леве до ниске са десне стране, попут нашег арапског система, али остатак ће вероватно бити непознат. Симбол за један је облик клина или И-облика. Нажалост, И такође представља 50. Постоји неколико засебних симбола (сви на основу клина и линије), али сви остали бројеви се формирају из њих.

Сјетите се облика писања клинопис или у облику клина. Због алата који се користи за цртање линија, постоји ограничена разноликост. Клин може или не мора имати реп, извучен повлачењем клијешта за писање дуж глине након утискивања дела троуглавог облика.

10, описано као стрелица, изгледа помало као

Три реда до 3 мала 1-а (написана као Ис са скраћеним реповима) или 10с (10 је написано као

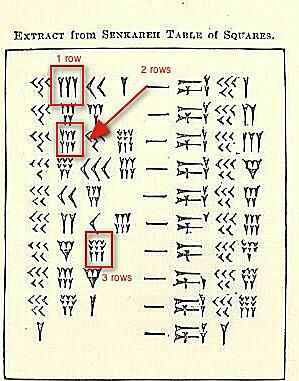
Постоје три скупа клинастог броја кластери истакнуто на горњој илустрацији.

Тренутно се не бавимо њиховом вредношћу, већ демонстрирањем како ћете видети (или писати) било где од 4 до 9 истог броја груписаних заједно. Три у низу. Ако постоји четврти, пети или шести, то иде испод. Ако постоји седми, осми или девети, потребан вам је трећи ред.

Следеће странице настављају са упутствима о обављању израчуна помоћу бабилонског клинописа.

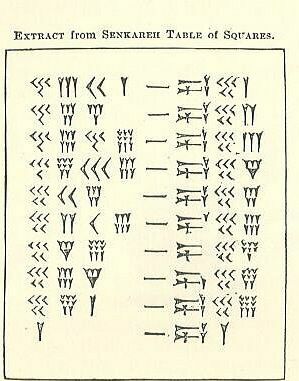
Из онога што сте прочитали горе о документу сосс - којега ћете памтити је Вавилоно 60 година, клин и стрелица - који су описни називи за клинописне знакове, погледајте да ли можете да схватите како функционишу та рачунања. Једна страна знака са цртицом је број, а друга је квадрат. Пробајте као група. Ако не можете да схватите, погледајте следећи корак.

Можете ли то сада схватити? Дајте шансу.

...

На левој страни су 4 јасна ступца, а иза њих је црта знак и десна 3 колона. Гледајући са леве стране, еквивалент колони 1с су заправо 2 колона најближа „цртици“ (унутрашњи ступац). Остала 2, спољна колона се рачунају заједно као колона 60-их.

• Тхе 4-
• 3-Ис = 3.
• 40+3=43.
• Једини проблем овде је што је иза њих још један број. То значи да нису јединице (место оних). 43 нису 43-их, већ 43-60-их, с обзиром да је сексуални систем (база-60) и налази се у сосс као што показује доња табела.
• Помножите 43 са 60 да бисте добили 2580.
• Додајте следећи број (2-
• Сада имате 2601.
• То је квадрат од 51.

Следећи ред има 45 у сосс па помножите 45 са 60 (или 2700), а затим додате 4 из колоне јединица, тако да имате 2704. Квадратни корен 2704 је 52.

Можете ли схватити зашто је последњи број = 3600 (60 у квадрату)? Савет: Зашто то није 3000?